Extracting Cryptographic Keys From Fuzzy Sources
By Amit Deo, PhD and Senior Cryptography Researcher. Amit takes us through methods for extracting cryptographic keys from fuzzy sources.
As outlined in a previous blog on using fingerprints for cryptography, being able to reliably extract cryptographic keys from noisy or “fuzzy” entropy sources is very useful in practice. A fairly common example of a noisy or fuzzy source would be a physical unclonable function or PUF where some characteristic property of a piece of hardware is measured to produce random bits. It is usually the case that the measurement results are not perfectly reproducible implying that PUFs are “fuzzy” sources. A more relatable example of a fuzzy source would be human fingerprint scans, where two readings of the same fingerprint may differ due to the presence of dust particles on the finger/reader.
As noted in the previous blog post, two common challenges when deriving cryptographic keys from fuzzy sources are:
- (Non-uniformity): How can we get a truly random secret key from a fuzzy source that is not truly random? In other words, how can we handle biases in the distribution of the fuzzy source?
- (Reproducibility): How can we be sure to re-derive the same key when measuring the fuzzy source many times?
Ultimately, the solution to both problems is to apply an algorithm called a “fuzzy extractor” to the fuzzy source readings. In this blog, we will look at the main techniques and reasoning used to build standard fuzzy extractors.
An important note: The two common challenges above do not apply to all PUF designs. For example, some PUFs are perfectly reproducible, and some are assumed to be uniform. This blog post considers any PUF where both challenges arise. However, cases, where just one of the challenges arise, can be handled by omitting and/or modifying certain techniques outlined in this blog post.
Suppose we have a fuzzy source and take two readings, the first will be called R1 and the second R2. Since the source is fuzzy, R1 will not be the same as R2, but they will be close. As an example, suppose that we interpret R1 and R2 as bit-strings. We might have R1 = “1 1 1 0 0 1 1 0 0 0” and R2 = “ 1 0 1 0 1 1 1 0 0 0” where the positions written in bold denote positions where R1 and R2 disagree. Fuzzy extractors allow us to initially use R1 to produce a cryptographic key K, and then, later on, use R2 to reproduce the same key K. This is achieved by storing a “hint” (also known as helper data) in non-volatile memory when K is first produced from R1. This same hint facilitates the reproduction of K from R2. To summarise, fuzzy extractors carry out two procedures that are pictorially represented in Figure 1:
- Initialise(R1): This uses R1 to output a cryptographic key K and a hint P
- Reproduce(R2, P): This uses R2 and the hint P to reproduce cryptographic key K.
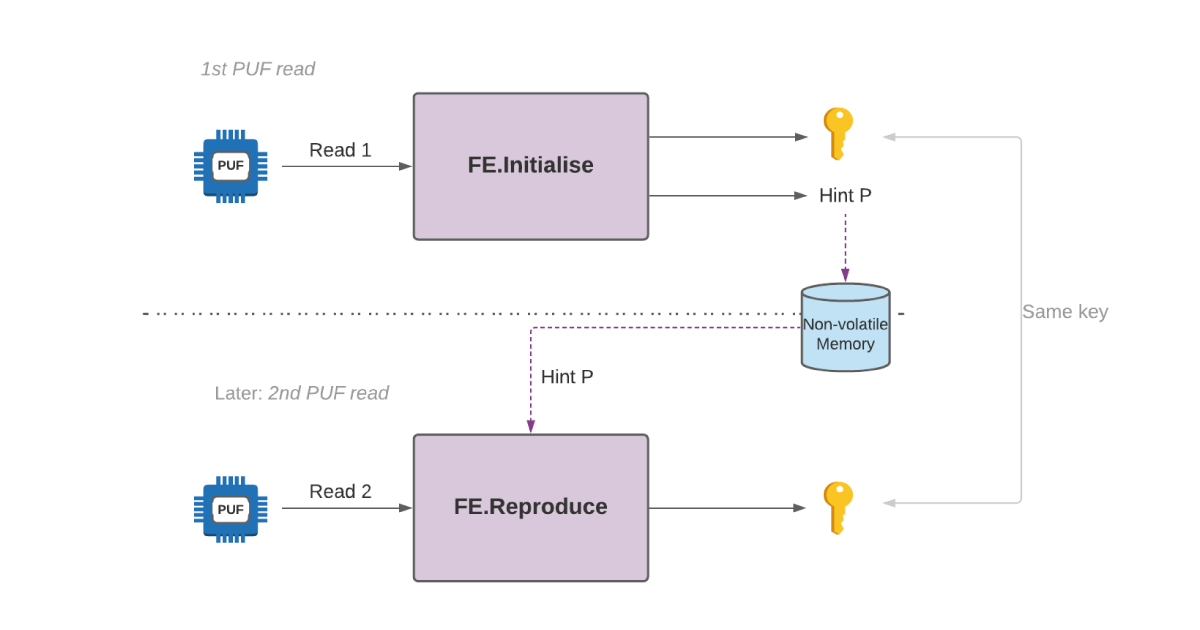
Important security consideration: It is usually assumed that the hint P is stored in non-volatile memory that may be accessible to a malicious attacker who wants to steal the key K. This means that revealing the hint in a good fuzzy extractor design should not make it easy to guess R1, R2 or K. Without this requirement, designing fuzzy extractors would be trivial – you could just use the derived key K as the hint.
How to produce hint P and use it to go from R2 to R1
Suppose we have bit-strings C1 and C2 that are “close” to each other, much like R1 and R2. Error-correcting codes are a very well-known method for recovering C1 from C2 when C1 is known to take a specific form (more precisely, when C1 is a codeword). Instead of defining an error-correcting code formally, we’ll just look at a simple example to provide intuition:
Example: Suppose that we know C1 is either “0 0 0 0 0 0 0 0 0 0” or “1 1 1 1 1 1 1 1 1 1” and that C2 is close but not the same as C1. Then we can simply recover C1 from C2 by checking whether C2 has more 0’s or more 1’s. For example, if C2 = “1 0 0 0 0 0 1 0 0 0”, we can be confident that C1 is “0 0 0 0 0 0 0 0 0 0”. On the other hand, if C2 = “1 1 1 1 1 0 0 1 1 1”, then C1 is likely to be all 1 string. The code here is known as a repetition code, and the method of obtaining C1 from C2 is known as the decoding procedure.
The example here is a simple case where C1 is allowed to take just one of two values. However, codes used in practice allow C1 to take a much larger number of values. Unfortunately, we cannot directly use error-correcting codes by treating R1 as C1 because the form of R1 does not take the special form. The way to get around this is to do the following to produce the hint:
- Pick a random C1 with the form specified by the error-correcting code (i.e. pick a truly random codeword). Using our simple example, we would pick C1 randomly as either “0 0 0 0 0 0 0 0 0 0” or “1 1 1 1 1 1 1 1 1 1”.
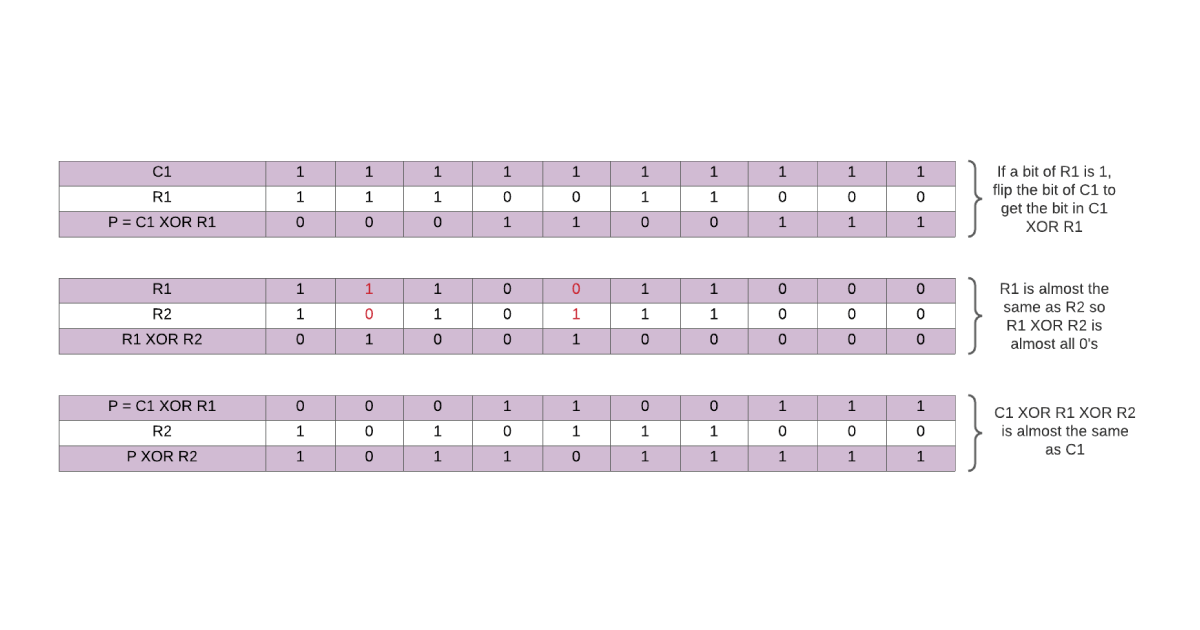
- Compute the hint P = C1 XOR R1. To compute C1 XOR R1, simply write down C1 and flip the first bit if the first bit of R1 is 1, flip the second bit of C1 if the second bit of R1 is 1 etc. See Figure 2 for examples.
An important thing to note about the XOR operation is that R1 XOR R1 = “0 … 0” and R1 XOR R2 is a string with just a few 1’s because R1 is nearly equal to R2. Now that we know how to produce a hint, let us see how to use the hint P and R2 to recover R1. To do this, we carry out the following steps:
- Compute C2 = P XOR R2 (this is equal to C1 XOR R1 XOR R2 which is roughly C1)
- Perform a decoding procedure on C2 to recover C1
- Then R1 = C1 XOR P (using the fact that P = C1 XOR R1)
Example: Suppose R1 = “1 1 1 0 0 1 1 0 0 0” and R2 = “ 1 0 1 0 1 1 1 0 0 0” and we use the repetition code from the previous example. When producing a hint, we first pick a random C1 i.e. randomly choose between “0 0 0 0 0 0 0 0 0 0” and “1 1 1 1 1 1 1 1 1 1”. Suppose we pick “1 1 1 1 1 1 1 1 1 1”. Then the hint is P = C1 XOR R1 = “0 0 0 1 1 0 0 1 1 1”.
When attempting to reproduce R1 from the hint P and second reading R2, we first compute C2 = P XOR R2 = “1 0 1 1 0 1 1 1 1 1” where the red positions are those in which C1 and C2 differ. Notice that C2 is almost the all 1 string, which means that from C2, we can conclude that C1 = “1 1 1 1 1 1 1 1 1 1”. Finally, we can recover R1 by computing C1 XOR P = “1 1 1 0 0 1 1 0 0 0”. See Figure 2 for this example with the XOR operations laid out more clearly.
An attacker that gets its hands on the hint P in the example poses a very serious security problem. The issue is that C1 can only take one of two values. This means that given a hint P, R1 can take one of just two values – R1 is either P XOR “1 1 1 1 1 1 1 1 1 1” or P XOR “0 0 0 0 0 0 0 0 0 0”. This is bad news as R1 is no longer unpredictable once the hint is leaked. However, the way to get around this issue is fairly simple – just use error-correcting codes where C1 can take an extremely large number of values. In practice, BCH codes can be a good choice due to their flexibility and efficient decoding procedures. Details on the code size requirements for a secure implementation are outside the scope of this blog post but can be derived from the Code-Offset construction in the seminal academic paper on fuzzy extractors.
How to go from R1 to K
We now look at the relatively simple question of how to translate R1 (that is not truly random) to a cryptographic key K that is truly random. One answer is to use a key derivation function or KDF. These are designed to take an unpredictable source (typically user-generated passwords) and output a cryptographic strength secret key K. In fact, KDFs even allow to derive long keys from relatively short user-generated passwords/secret information. For more details on KDFs, see the blog post here. There are also other options for this step with different security assumptions/trade-offs that are not covered in this blog.
Conclusion: Putting everything together to build a fuzzy extractor
We have now seen how to take a hint P and second reading R2 to recover R1 in Part I, and then how to produce a cryptographic strength key K from R1 in Part II. We can now put everything together to describe the two algorithms that make up a fuzzy extractor:
- Initialise(R1): Uses R1 to output a cryptographic key K using a KDF on R1 (see Part II) and a hint P (using the technique from Part I).
- Reproduce(R2, P): Uses R2 and the hint P (as described in Part I) to reproduce R1 and then uses a KDF on R1 (see Part II) to reproduce K.
The techniques described in this blog roughly describe the most commonly used construction of a fuzzy extractor called the “code offset” construction. The reason for this name is that when producing the hint, we simply XOR C1 (i.e. a random codeword) to R1. In other words, we “offset” the reading R1 by a random codeword C1 to produce a hint.
There are also other possible constructions. Some of these build upon similar ideas but aim to provide stronger security guarantees. For example, there are slightly more complex constructions that enable the detection of corrupted/maliciously modified hints (these are called robust fuzzy extractors). There are also constructions preserving key secrecy when an attacker has access to multiple hints derived from the same source (these are called reusable fuzzy extractors). Therefore, the techniques outlined in this blog post should serve as a mere introduction to the world of fuzzy extractors rather than a detailed account of them.
Additional resources
Whitepaper
Enabling Cloud Connectivity in Resource-Constrained IoT Devices: A Wi-Fi Module and Low-End MCU Approach
This paper explores an affordable and efficient approach to embedded device cloud connectivity using a Wi-Fi module with a low-end microcontroller unit…
Read more
Whitepaper
Hardware Root of Trust: QDID PUF & Attopsemi OTP
This whitepaper presents a simplified, secure, and ready-to-use root-of-trust solution for embedded devices by integrating Attopsemi’s I-fuse technology…
Read more
Whitepaper
QuarkLink for Industrial PCs
This white paper introduces how Crypto Quantique’s QuarkLink SaaS device security platform is used with industrial PCs running Linux.
Read more

